4  Simple linear regression

This chapter is a work in progress.

Learning goals

• Use exploratory data analysis to assess whether a simple linear regression is an appropriate model to describe the relationship between two variables
• Estimate the slope and intercept for a simple linear regression model
• Interpret the slope and intercept in the context of the data
• Use the model to compute predictions and residuals
• Calculate and interpret $R^2$ and RMSE in the context of the data
• Conduct simple linear regression using R

Software and packages

• library(tidyverse) (Wickham et al. 2019)

• library(patchwork) (Pedersen 2022)

• library(skimr) (Waring et al. 2022)

• library(broom) (Robinson, Hayes, and Couch 2023)

• library(yardstick) (Kuhn, Vaughan, and Hvitfeldt 2025a)

4.1 Introduction: Movie ratings on Rotten Tomatoes

Reviews from movie critics can be helpful information when determining whether a movie is high quality and well-made; however, it can be challenging to determine whether regular audience members will like a movie based on critics reviews. You decide to use simple linear regression to better understand the relationship between what movie critics and regular movie-goers think about a movie, so you can ultimately predict how an audience will rate a movie based on its score from movie critics.

The movie_scores data includes the critics and audience scores for 146 movies released in 2014 and 2015 . These are every movie released in these years that have “a rating on Rotten Tomatoes, a RT User rating, a Metacritic score, a Metacritic User score, an IMDb score, and at least 30 fan reviews on Fandango” (Albert Y. Kim, Ismay, and Chunn 2018a). The analysis in this chapter focuses on scores from Rotten Tomatoes, a website for information and ratings on movies and television shows. The data were originally analyzed in the article “Be Suspicious of Online Movie Ratings, Especially Fandango’s” (Hickey 2015) on the former data journalism site FiveThirtyEight. The data set is movie_scores.csv ; it was adapted from the fandago data frame in the fivethirtyeight R package (Albert Y. Kim, Ismay, and Chunn 2018b).

We will focus on two variables for this analysis:

• critics: Critics score calculated as the percentage of critics who have a favorable review of the movie. This is known as the “Tomatometer” score on the Rotten Tomatoes website. The possible values are 0 - 100.

• audience: Audience score calculated as the percentage of users on the site (regular movie-goers) who have a favorable review of the movie. The possible values are 0 - 100.

The objective of this analysis is to model the relationship between the critics score and audience score using simple linear regression. We want to use the model to

• describe how the audience score is expected to change as the critics score changes.

• predict the audience score for a movie based on its critics score.

Before taking a look at the data, let’s define two terms that will be important for this chapter and the rest of the text. The response variable is the outcome of interest. It is also known as the outcome or dependent variable and is represented as $Y$. The predictor variable(s) is the variable (or variables) used to understand variability in the response. It is also known as the explanatory or independent variable and represented as $X$. The observed values of the response and predictor are represented as $y_i$ and $x_i$, respectively.

In this chapter, we will fit and analyze models with one predictor variable. We will extend to the case of multiple predictor variables in Chapter 7.

Your turn!

What is the response variable for the movie scores analysis? What is the predictor variable?¹

4.2 Exploratory data analysis

Recall from Chapter 3 that every analysis starts with exploratory data analysis (EDA) to better understand the observations in the data, the distributions of the variables, and to gain initial insights about the relationships between the variables of interest. EDA can also help us identify outliers or other unusual observations, missing data, and potential errors in the data, such as errors in how the data were recorded or how the data set was loaded into the statistical software.

The exploratory data analysis here only focuses only on the two variables that will be in the regression model, critics and audience. In practice, however, we may want to explore other variables in the data set (for example, year in this analysis) to provide additional context later on as we interpret results from the regression model. We begin with univariate EDA, exploring one variable at a time, then we’ll conduct bivariate EDA to look at the relationship between critics and audience scores.

4.2.1 Univariate EDA

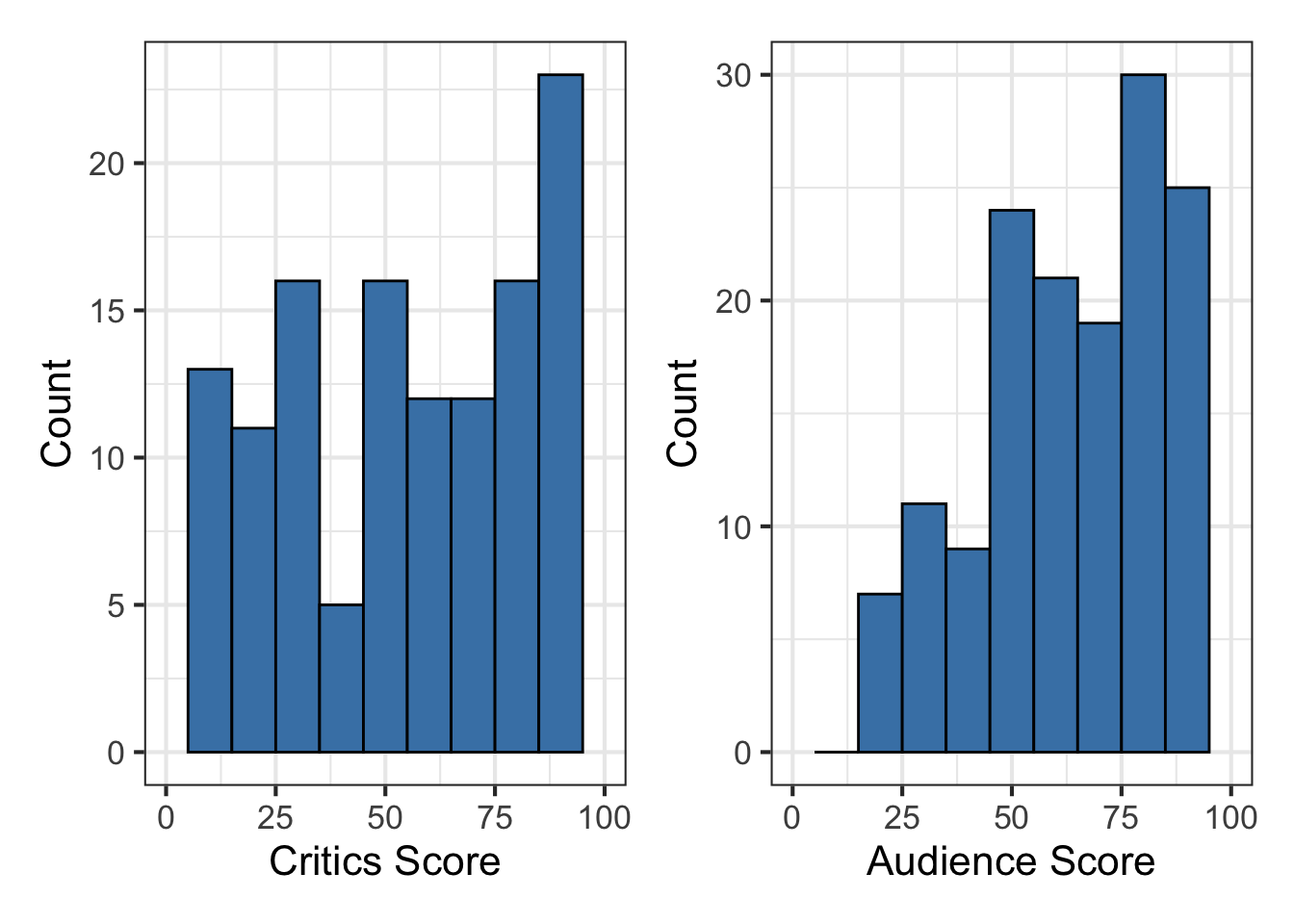
The univariate distributions of the critics and audience scores are visualized in Figure 4.1 and summarized in Table 4.1.

Figure 4.1: Univariate distributions of critics scores and audience scores for movies on Rotten Tomatoes.

Table 4.1: Summary statistics for audience and critics score

Variable	Mean	SD	Min	Q1	Median (Q2)	Q3	Max	Missing
critics	60.8	30.2	5	31.2	63.5	89	100	0
audience	63.9	20.0	20	50.0	66.5	81	94	0

The distribution of critics is left-skewed, meaning the movies in the data set are generally more favorably reviewed by critics (more observations with higher critics scores). Given the apparent skewness, the center is best described by the median score of 63.5 points. The interquartile range (IQR), the spread of the middle 50% of the distribution, is 57.8 points $(Q_3-Q_1=89-31.2)$, so there is a lot of variability in the critics scores for the movies in the data. There are no apparent outliers, but we observe from the raw data that there are two notable observations of movies that have perfect critics scores of 100. There are no missing values of critics score.

Your turn!

Use the histogram in Figure 4.1 and summary statistics in Table 4.1 to describe the distribution of the response variable audience.

4.2.2 Bivariate EDA

After we’ve examined the variables individually, we begin to explore the relationships between variables. We’ll focus on the relationship between the response and predictor variable for our model; however, there may be other variable relationships we want to understand to provide additional context to the results from the regression model.

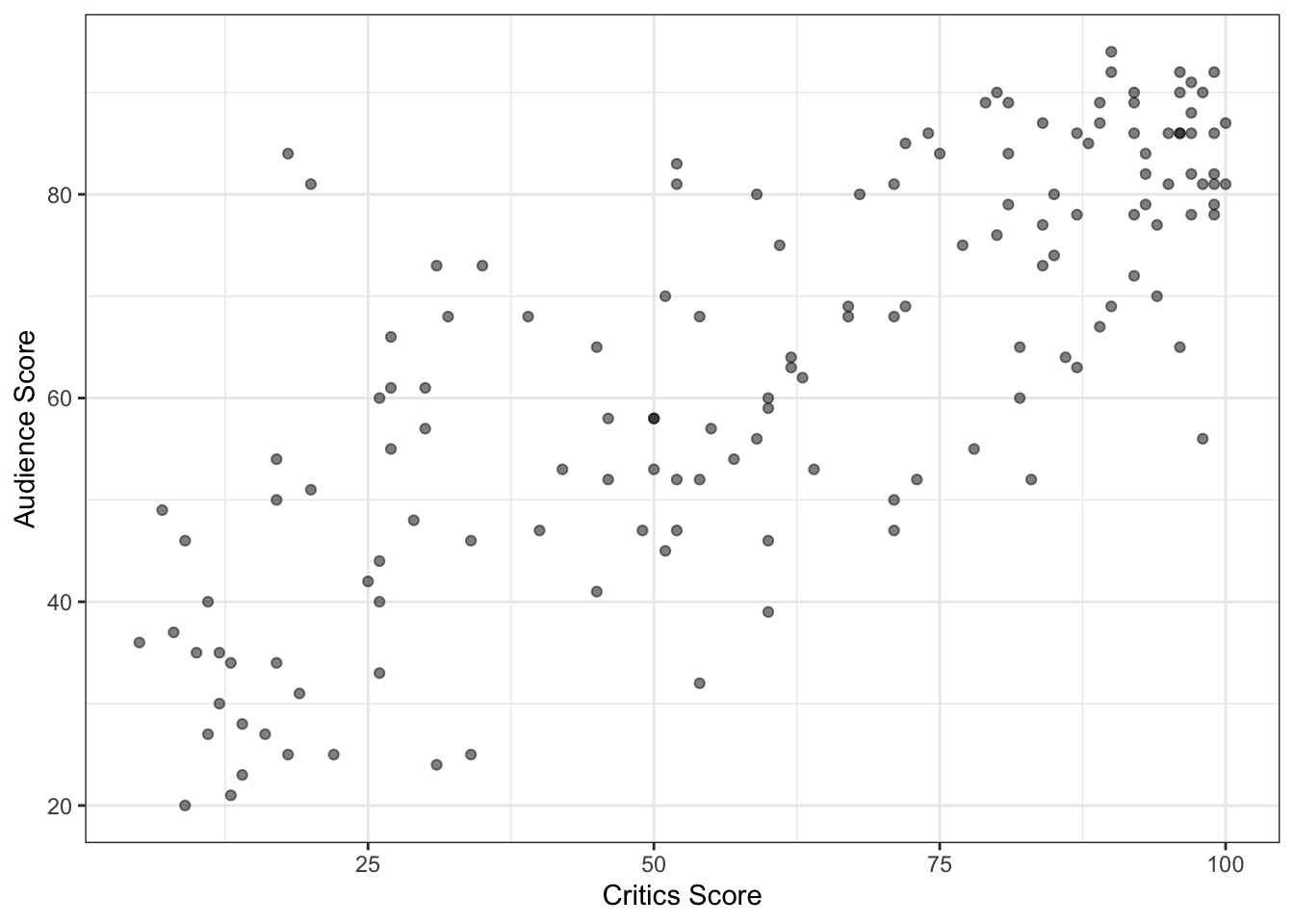
As introduced in Chapter 3, we visualize the relationship between variables and calculate summary statistics to better quantify the relationships. A scatterplot of the the audience score versus critics score is shown in Figure 4.2. When making the scatterplot, we put the predictor variable on the $x$-axis (horizontal axis) and the response variable on the $y$-axis (vertical axis).

Figure 4.2: Scatterplot of critics and audience scores for movies on Rotten Tomatoes.

There is a positive, linear relationship between the critics and audience scores for movies on Rotten Tomatoes. The correlation between these two variables is 0.78, indicating the relationship is moderately strong. Therefore, we can generally expect the audience score to be higher for movies with higher critics scores. There are no apparent outliers, but there does appear to be more variability in the audience score for movies with lower critics scores than for those with higher critics scores.

4.3 Linear regression

As we saw in Section 4.2, we can use visualizations and summary statistics to describe the relationship between two variables. The exploratory data analysis, however, does tell us what the response is predicted to be for a given value of the predictor or how much the response is expected to change as the predictor changes. Therefore, we will fit a linear regression model to the data and quantify the relationship between the response and predictor variable. More specifically, we will fit a model of the form

$$\begin{array}{}\text{(4.1)}& Y={\beta }_0+{\beta }_{1}X+ϵ\end{array}$$

Equation 4.1, called a simple linear regression (SLR) model, is the equation of a line representing the relationship between one response variable and one predictor variable. For now we will focus on models with one quantitative (numeric) response and one quantitative predictor variable. In later chapters, we will introduce categorical predictors, models with two or more predictors, and models with a categorical response variable.

We are generally interested in using regression models for two types of tasks:

• Prediction: Finding the expected value of the response variable for given values of the predictor variable(s).
• Inference: Drawing conclusions about the relationship between the response and predictor variable(s).

Your turn!

We will fit a simple linear regression line to describe the relationship between the critics scores and audience scores for movies.

• What is an example of a prediction question that can be answered using a simple linear regression model?²

• What is an example of an inference question that can be answered using a simple linear regression model?³

4.3.1 Statistical model

Suppose there is a response variable $Y$ and a predictor variable $X$. The values of the response variable $Y$ can be generated in the following way:

$$Y=Model+Error$$

More specifically, we define the model as a function of the predictor $X$, $Model=f(X)$, and error $ϵ$, such that

$$\begin{array}{}\text{(4.2)}& Y=f(X)+ϵ\end{array}$$

The function $f(X)$ that describes the relationship between the response and predictor variable is the regression model. This is the model we will fit in later sections using equations and R. The error, $ϵ$, is how much the actual value of the response $Y$ deviates from the value produced by the regression model. There is some randomness in $ϵ$ , because not all observations with the same value of $X$ have the same value of $Y$. For example, not all movies with a critics score of 70 have the same audience score.

Equation 4.2 is the general form of the equation to generate values of $Y$ given values of $X$. In the context of simple linear regression, the function $f(X)$ in Equation 4.2 is

$$\begin{array}{}\text{(4.3)}& f(X)={\mu }_{Y|X}={\beta }_0+{\beta }_{1}X\end{array}$$

where ${\mu }_{Y|X}$ is the mean value of $Y$ at a particular value of $X$. The error terms $ϵ$ from Equation 4.2 are normally distributed with a mean of 0 and variance ${\sigma }_{ϵ}^2$, represented as $N(0,{\sigma }_{ϵ}^2)$. The full specification of the simple linear regression model is shown in Equation 4.4. This may look familiar, as the function was originally presented in Equation 4.1; here we have completed the specification of the simple linear regression model with the inclusion of the distribution of the error terms. It is written in terms of an individual observation with response $y_i$, predictor $x_i$, and error ${ϵ}_i$.

$$\begin{array}{}\text{(4.4)}& y_i={\beta }_0+{\beta }_1{x}_i+{ϵ}_i{ϵ}_i\sim N(0,{\sigma }_{ϵ}^2)\end{array}$$

Equation 4.4 is the statistical model, also called the data-generating model. It is the population-level model that describes exactly how to generate the values of the response $Y$ given values of the predictor in the population. In this model, ${\beta }_0$ is called the intercept, ${\beta }_1$ is called the slope, and ${\sigma }_{ϵ}^2$ is called the standard error. In practice we don’t know the exact values of ${\beta }_0$, ${\beta }_1$, and ${\sigma }_{ϵ}^2$, so our goal is to use sample data to estimate these values. In the remainder of this chapter we’ll focus on estimating ${\beta }_0$ and ${\beta }_1$. We’ll discuss ${\sigma }_{ϵ}^2$ in more detail in Chapter 5.

Review

The population is the group we’re interested in understanding using statistical analysis. This could be a group of people, places, objects, etc.

The sample is the subset of the population on which we have data for the analysis. We analyze the sample data to derive insights about the population. Ideally the sample has been generated in a way that it is representative of the population. This enables us to draw more conclusions that can be generalized to the population.

What is the population in the movie scores analysis? What is the sample?⁴

Now that we have specified the form of the model, we will evaluate whether a model of this form is an appropriate choice for the data.

4.3.2 Evaluating whether SLR is appropriate

Before doing any more calculations, we need to determine if the simple linear regression model is a reasonable choice for the data based on what we know about the data and what we’ve observed from the exploratory data analysis. We will evaluate the model fit more thoroughly in later analysis steps. The questions can help prevent going in a wrong analysis direction is a linear regression model is obviously not a good choice for the data.

• Will a linear regression model be practically useful? Does quantifying and interpreting the relationship between the variables make sense in this scenario?
• Is the shape of the relationship reasonably described by a linear model? In the context of simple linear regression, does a line reasonably describe the relationship?
• Do the observations in the data represent the population of interest, or are there biases in the data that could limit conclusions drawn from the analysis?

Warning

Mathematical equations or statistical software can be used to fit a linear regression model between any two quantitative variables. It is upon the judgment of the analyst to determine if it is reasonable to proceed with a linear regression model or if doing so might result in misleading conclusions about the data.

If the answer is “no” to any of the questions above, consider if a different analysis technique is better for the data, or proceed with caution if using regression. If you proceed with regression, be transparent about some of the limitations of the conclusions.

As described in Section 4.1, the goal of this analysis is understand the relationship between the critics scores and audience score for movies on Rotten Tomatoes. Therefore, there is a practical use for fitting the regression model. We observed from Figure 4.2 that the relationship between the two variables is approximately linear, so it could reasonably be summarized using a line. Lastly, the data set includes all movies in 2014 and 2015 that were rated on popular movie ratings websites, so we can reasonably conclude the sample is representative of the population of movies on Rotten Tomatoes. Therefore, we are comfortable drawing conclusions about the population based on the analysis of our sample data.

The simple linear regression model for the movie scores data has the form

$$\begin{array}{}\text{(4.5)}& audience={\beta }_0+{\beta }_{1}critics+ϵ,ϵ\sim N(0,{\sigma }_{ϵ}^2)\end{array}$$

Now let’s discuss how to estimate the slope ${\beta }_1$ and the intercept ${\beta }_0$. We will estimate ${\sigma }_{ϵ}^2$ in Chapter 5.

4.4 Estimating slope and intercept

Ideally, we would have data from the entire population of movies rated on Rotten Tomatoes in order to calculate the exact values for ${\beta }_1$, ${\beta }_0$, and ${\sigma }_{ϵ}^2$. In reality we don’t have access to the data from the whole population, but we can use the sample to obtain the estimated regression equation in Equation 4.6.
$$\begin{array}{}\text{(4.6)}& {\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{x}_i,\end{array}$$

where ${\hat{\beta }}_0$ is the estimated intercept, ${\hat{\beta }}_1$ is the estimated slope, and $\hat{y}$ is the predicted (estimated) response and $x_i$ is the value of the predictor variable. The subscript $i$ denotes the $i^{th}$ observation.

Specifically for the movie scores analysis, the estimated regression equation is

$$\begin{array}{}\text{(4.7)}& {\widehat{audience}}_i=32.3155+0.5187critic{s}_i\end{array}$$

In this equation 32.3155 is ${\hat{\beta }}_0$, the estimated value for the intercept, 0.5187 is ${\hat{\beta }}_1$, the estimated value for the slope ${\beta }_1$, and ${\widehat{audience}}_i$ is the expected audience score when the critics score is equal to $critic{s}_i$. Notice that Equation 4.6 and Equation 4.7 do not have have error terms. The output from the regression equation is the expected mean value of the response for a given value of the predictor. Therefore, when we discuss the values of the response estimated using simple linear regression, what we are really talking about is what the value of the response variable is expected to be, on average, for a given value of the predictor variable.

From Figure 4.2, we know that the value of the response is not necessarily the same for all observations with the same value of the predictor. For example, we wouldn’t expect (nor do we observe) the same audience score for every movie with a critics score of 70. We know there are other factors other than the critics score that are related to how an audience reacts to a movie. Our analysis, however, only takes into account the critics score, so we do not capture these additional factors in our regression equation Equation 4.7. This is where the error terms come back in.

Once we computed estimates ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$ for the regression equation, we can calculate how far the predicted values of the response produced by the regression equation differ from the actual values of the response variable observed in the data. This difference is called the residual.

Terminology

The residual is the difference between the observed and predicted values of the response for a given observation.

$$residua{l}_i=observe{d}_i-predicte{d}_i$$

Equation 4.8 shows the equation of the residual for the $i^{th}$ observation.

$$\begin{array}{}\text{(4.8)}& e_i=y_i-{\hat{y}}_i\end{array}$$

In the case of the movie scores data, the residual is the difference between the actual audience score and the audience score predicted by Equation 4.7. For example, the 2015 movie Avengers: Age of Ultron received a critics score of $y_i=74$. Therefore, using Equation 4.7, the estimated (predicted) audience score is.

$${\hat{y}}_i=32.3155+0.5187\times 74=70.6993.$$

The observed audience score is 86, and the residual is

$$e_i=y_i-{\hat{y}}_i=86-70.6993=15.3007$$

Your turn!

Would you rather see a movie that has a positive or negative residual? Explain your response.

4.4.1 Least squares regression

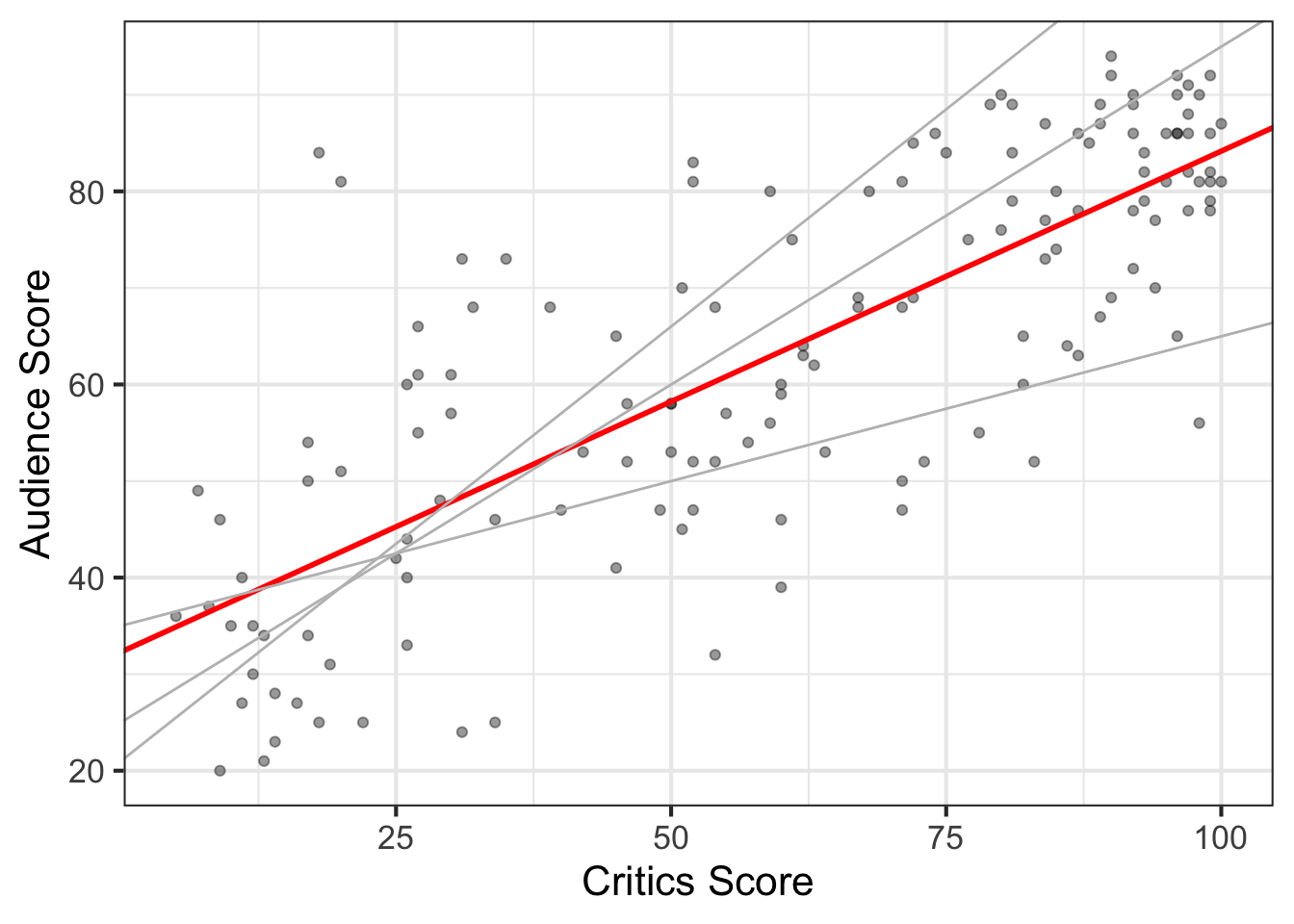
As shown in Figure 4.3, there are many possible lines (infinitely many, in fact) that we could use to describe the relationship between the critics and audience scores. So how did we determine the line that “best” fits the data is the one described by Equation 4.7? We’ll use the residuals to help us answer this question.

Figure 4.3

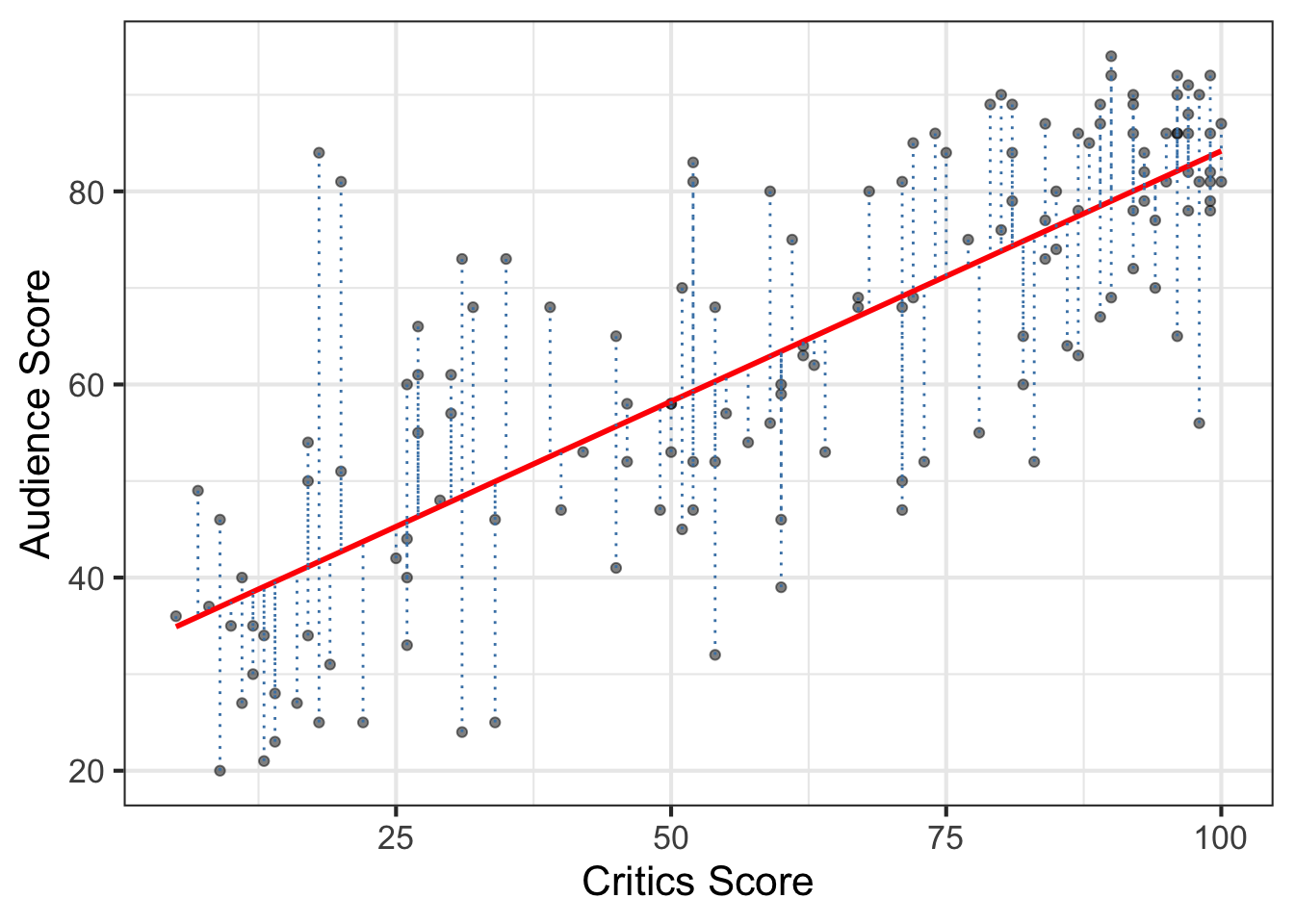
The residuals, represented by the vertical dotted lines in Figure 4.4, are a measure of the “error”, the difference between the observed value of the response and the value predicted from a regression model. The line that “best” fits the data is the one that generally results in the smallest overall error. One way to find the line with the smallest overall error is to add up all the residuals for each possible line in Figure 4.3 and choose the one that has the smallest sum. Notice, however, that for lines that seem to closely align with the pattern of the observations in the data, there is approximately equal distribution of points above and below the line. Thus as we’re trying to compare lines that pretty closely fit the data, we’d expect the residuals to add up to a value very close to zero. This would make it difficult, then, to determine a best fit line.

Figure 4.4

Instead of using the sum of the residuals, we will instead consider the sum of the squared residuals, $e_1^2+e_2^2+\cdots +e_n^2$ , where $n$ is the number of observations in the data. The line that “best” fits the data, then, is the line with the smallest sum of squared residuals. This process is called least squares regression.

Terminology

The least squares regression line is the line, ${\hat{\beta }}_0+{\hat{\beta }}_{1}X$ , that minimizes the sum of the squared residuals.

We use this objective of minimizing the the sum of squared residuals to find the estimates ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$. Recall that $e_i$, the residual of the $i^{th}$ observation, is $y_i-{\hat{y}}_i$ where ${\hat{y}}_i$ is the estimated response. Filling in the regression equation Equation 4.6, we have

$$\begin{array}{}\text{(4.9)}& \begin{array}{rl}{e}_i& =y_i-{\hat{y}}_i\\ & =y_i-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_i)\end{array}\end{array}$$

Extending Equation 4.9 to all observations and taking the sum of the squared residuals, we have

$$\begin{array}{}\text{(4.10)}& \begin{array}{rl}\sum _{i=1}^n{e}_i^2& =e_1^2+e_2^2+\cdots +e_n^2\\ & =[y_1-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_1){]}^2+[y_2-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_2){]}^2+& \\ & \cdots +[y_n-({\hat{\beta }}_0+{\hat{\beta }}_1{x}_n){]}^2\end{array}\end{array}$$

Using calculus, the values of ${\beta }_0$ and ${\beta }_1$ that minimize Equation 4.10 are

$$\begin{array}{}\text{(4.11)}& {\hat{\beta }}_1=r\frac{s_Y}{s_X}{\hat{\beta }}_0=\overline{y}-{\hat{\beta }}_1\overline{x}\end{array}$$

where $\overline{x}$ and $\overline{y}$ are the mean values of the predictor and response variables, respectively, $s_X$ and $s_Y$ are the standard deviations of the predictor and response variables, respectively, and $r$ is the correlation between the response and predictor variables. See Appendix A.1 for the full details of the derivation from Equation 4.10 to Equation 4.11.

The calculations for the slope and intercept for the movie scores model in Equation 4.7 based on the values in Section 4.2 are below. Note that the small differences in the values compared to Equation 4.7 are due to using rounded rather than exact values to compute the estimates.

$$\begin{array}{rl}{\hat{\beta }}_1& =0.78\times \frac{20.0}{30.2}=0.517\\ {\hat{\beta }}_0& =63.9-0.517\times 60.8=32.467\end{array}$$

Properties of least squares regression

• The regression line goes through the center of mass point, the coordinates corresponding to average $X$ and average $Y$: ${\hat{\beta }}_0=\overline{Y}-{\hat{\beta }}_1\overline{X}$

• The slope has the same sign as the correlation coefficient: ${\hat{\beta }}_1=r\frac{s_Y}{s_X}$

• The sum of the residuals is zero: $\sum _{i=1}^n{e}_i=0$

• The residuals and predictor ($X$) values are uncorrelated

4.4.2 Fitting the least-squares line in R

We fit linear regression models using the lm function, which is part of the stats package (2024). We then use the tidy function from the broom package (Robinson, Hayes, and Couch 2023) to display the results in a tidy format in which each row is a term in the model and each column is a property of that term.

Begin by using thelibrary function to load broom into the R environment. The stats package is automatically into the R environment when R is opened, so we don’t need to load it here.

library(broom)

The code to find the linear regression model using the movie_scores data with audience as the response and critics as the predictor (Equation 4.7) is below.

lm(audience ~ critics, data = movie_scores)

Call:
lm(formula = audience ~ critics, data = movie_scores)

Coefficients:
(Intercept)      critics  
    32.3155       0.5187  

Next, we wan to display the model results in a tidy format. We build upon the code above by saving the model in an object called movie_fit and displaying the object. We will also use movie_fit to calculate predictions.

1movie_fit <- lm(audience ~ critics, data = movie_scores)
2tidy(movie_fit)

1

Save the model output as movie_fit.

2

Display the model output in a tidy format.

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   32.3      2.34        13.8 4.03e-28
2 critics        0.519    0.0345      15.0 2.70e-31

Notice the resulting the model is the same as Equation 4.7, which we calculated based on Equation 4.11.

4.5 Interpreting slope and intercept

The slope ${\hat{\beta }}_1$ is the estimated change in the response for each unit increase in the predictor variable. What do we mean by “estimated change”? Recall that the output from the regression equation is ${\mu }_{Y|X}$ the estimated mean of the response $Y$ for a given value of the predictor $X$. Thus, the slope or the “steepness” of the regression line, is a measure of how much the response variable is expected to change, on average, for each unit increase of the predictor.

It is good practice to write the interpretation of the slope in the context of the data, so that it can be more easily understood others reading the analysis results. “In the context of the data” means that the interpretation includes

• meaningful descriptions of the variables, if the variable names would be unclear to an outside reader
• units for each variable
• an indication of the population for which this model applies.

The slope in Equation 4.7 of 0.5187 is interpreted as the following:

For each additional point in the critics score, the audience score for movies on Rotten Tomatoes is expected to increase by 0.5187 points, on average.

The intercept is the estimated value of the response variable when the predictor variable equals zero $(X=0)$. On a scatterplot of the response and predictor variable, this is the point where the regression line crosses the $y$-axis. Similar to the slope, the “estimated value” is more specifically the estimated mean value of the response variable when $X=0$ ( ${\hat{\mu }}_{Y|X=0})$.

The intercept in Equation 4.7 of 32.3155 is interpreted as the following:

The expected audience score for movies on Rotten Tomatoes with a critics score of 0 is 32.3155 points.

We always need to include the intercept to compute the line that best fit using least squares regression. The intercept, however, does not always have a meaningful interpretation. The intercept has a meaningful interpretation if the following are true.

1. It is plausible for the predictor variable to take values at or near zero.

2. There are observations in the data with values of the predictor at or near zero.

If either of these is not true, then it is not meaningful, and potentially misleading, to interpret the intercept.

Your turn!

What is the value of the intercept? Interpret this value in the context of the data. Is the interpretation of the intercept in Equation 4.7 meaningful? Briefly explain.⁵

Avoid making causal (or declarative) statements!

Avoid using causal language and making declarative statements when interpreting the slope and intercept. Remember the slope and intercept are estimates describing what we expect the relationship between the response and predictor to be based on the sample data and linear regression model. They do not tell us exactly what will happen in the data. We would need to analyze all data in the population to know the exact values!

4.6 Prediction

In Section 4.3, we introduced two main uses for a regression analysis: prediction and inference. We will talk more about inference in Chapter 5 and focus on prediction for now.

When a regression model is used for prediction, the estimated value of the response variable is computed based on a given value of the predictor. We’ve seen this in earlier sections when calculating the residuals. Let’s take a look at the model predictions for two movies released in 2023.

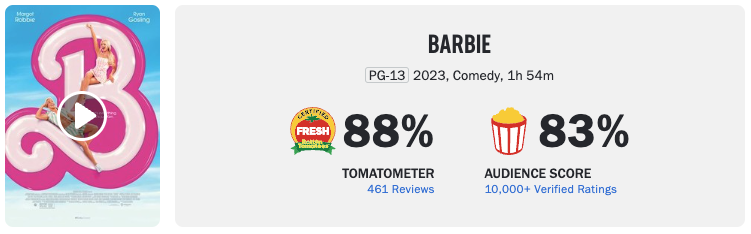
The movie Barbie was released in theaters on July 21, 2023. This movie was widely praised by critics, and it has a critics score of 88 at the time the data were obtained. Based on Equation 4.7, the predicted audience score is

$$\begin{array}{rl}\widehat{audience}& =32.3155+0.5187\times 88\\ & =\mathbf{\text{77.9611}}\end{array}$$

From the snapshot of the Barbie Rotten Tomatoes page (Figure 4.5), we see the actual audience score is 83⁶. Therefore, the model under predicted the audience score by about 5 points (83 - 77.9611). Perhaps this isn’t surprising given this film’s massive box office success!

Figure 4.5: Source: https://www.rottentomatoes.com/m/barbie (accessed August 29, 2023)

Your turn!

The movie Asteroid City was released in theaters on June 23, 2023. The critics score for this movie was 75⁷.

• What is the predicted audience score?

• The actual audience score is 62. Did the model over or under predict? What is the residual? ⁸

The regression model is most reliable when predicting the response for values of the predictor within the range of the sample data used to fit the regression model. Using the model to predict for values far outside this range is called extrapolation. The sample data provide information about the relationship between the response and predictor variables for values within the range of the predictor in the data. We can not safely assume that the linear relationship quantified by our model is the same for values of the predictor far outside of this range. Therefore, extrapolation often results in unreliable predictions that could be misleading if the linear relationship does not hold outside the range of the sample data.

Avoid extrapolation!

Only use the regression model to compute predictions for values of the predictor that are within (or very close) to the range of values in the sample data used to fit the model. Extrapolation, using a model to compute predictions for value so the predictor far outside the range in the data, can result in unreliable predictions.

4.6.1 Computing predictions in R

Below is the code to predict the audience score for Barbie as shown earlier in the section. Recall from Section 4.4.2 that the movie scores model produced by the lm() function is saved as movie_fit.

1barbie_movie <- tibble(critics = 88)
2predict(movie_fit, barbie_movie)

1

Create a tibble (Müller and Wickham 2023) that contains the critics score for Barbie. A tibble is a data frame that modifies “some older behaviours to make life a little easier”(Wickham, Çetinkaya-Rundel, and Grolemund 2023). Note that the name of the column in the tibble must exactly match the name of the predictor in the lm() code to fit the model.

2

The first argument of the predict function is the object containing the model fit. The second argument is the newly created tibble line (1).

       1 
77.95917 

We can produce predictions for multiple movies by putting multiple values of the predictor in the tibble. In the code below we produce predictions for Barbie and Asteroid City.

1new_movies <- tibble(critics = c(88, 75))
2predict(movie_fit, new_movies)

1

Create a vector that contains the values of the predictor for the two observations we want to predict. As before, the name of the column in the tibble must exactly match the name of the variable in the lm() code.

2

Calculate predictions for each value in new_movies.

       1        2 
77.95917 71.21636 

4.7 Model evaluation

We have shown how a simple linear regression model can be used to describe the relationship between a response and predictor variable and to predict new values of the response. Now we will look at two statistics that will help us evaluate how well the model fits the data and how well it explains variability in the response.

4.7.1 Root Mean Square Error

The Root Mean Square Error (RMSE), shown in Equation 4.12, is a measure of the average difference between the observed and predicted values of the response variable.

$$\begin{array}{}\text{(4.12)}& RMSE=\sqrt{\frac{\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}{n}}=\sqrt{\frac{\sum _{i=1}^n{e}_i^2}{n}}\end{array}$$

This measure is especially useful if prediction is the primary modeling objective. The RMSE takes values from 0 to $\mathrm{\infty }$ (infinity) and has the same units as the response variable.

Your turn!

Do higher or lower values of RMSE indicate a better model fit?⁹

There is no universal threshold of RMSE to determine whether the model is a good fit. In fact, the RMSE is often most useful when comparing the performance of multiple models. When using RMSE to assess a model fit, take the following into account:

1. What is the range (max value - min value) of the response variable in the data? How does the RMSE compare to the range? On average, what is the error percentage?
2. What is a reasonable error threshold based on the subject matter and analysis objectives? For example, you may be willing to use a model with higher RMSE for a low-stakes analysis objective (for example, the model is used to inform the choices of movie-goers) than a high-stakes objective (the model is used to inform how a movie studio’s multi-million dollar marketing budget will be allocated).

Your turn!

The RMSE for the movie scores model is 12.452. The range for the audience score is 74. What is your evaluation of the model fit based on RMSE? Explain your response.

4.7.2 Analysis of variance and $R^2$

The coefficient of determination, $R^2$, is a measure of the percentage of variability in the response variable that is explained by the predictor variable. Before talking more about how $R^2$ is used for model evaluation, let’s discuss how this percentage is calculated.

There is variability in the response variable, as we see in the exploratory data analysis in Figure 4.1 and Table 4.1 . Analysis of Variance (ANOVA), Equation 4.13, is the process of partitioning the various sources of variability.

$$\begin{array}{}\text{(4.13)}& \text{Total variability}=\text{Explained variability}+\text{Unexplained variability}\end{array}$$

The variability in the response variable is from two sources:

1. Explained variability (Model): This is the variability in the response variable that can be explained from the model. In the case of simple linear regression, it is the variability in the response variable that can be explained by the predictor variable. In the movie scores analysis, this is the variability in the audience score that is explained by the critics score.

2. Unexplained variability (Residuals): This is the variability in the response variable that is left unexplained after the model is fit. This can be understood by assessing the variability in the residuals. In the movie scores analysis, this is the variability due to the factors other than critics score and randomness.

The variability in the response variable and the contribution from each source is quantified using sum of squares. In general, the sum of squares (SS) is a measure of how far the observations are from a given point, for example the mean. Using sum of squares, we can quantify the components of Equation 4.13.

Let $SST$ = Sum of Squares Total, $SSM$ = Sum of Squares Model, and $SSR$ = Sum of Squares Residuals. Then,

$$\begin{array}{}\text{(4.14)}& \begin{array}{rl}SST& =SSM+SSR\\ \sum _{i=1}^n(y_i-\overline{y}{)}^2& =\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2+\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2\end{array}\end{array}$$

Sum of Squares Total (SST) $=\sum _{i=1}^n(y_i-\overline{y}{)}^2$, is the total variability, an overall measure of how far the observed values of the response variable are from the mean value of the response $\overline{y}$. The formula for SST may look familiar, as it is $(n-1)s_y^2$ , which equals$(n-1)$ times the variance of $y$. SST can be partitioned into two pieces, Sum of Squares Model (SSM) and Sum of Squares Residuals (SSR).

Sum of Squares Model (SSM) $=\sum _{i=1}^n({\hat{y}}_i-\overline{y}{)}^2$, is the explained variability, an overall measure of how much the predicted value of the response variable (the expected mean value of the response given the predictor) differs from the overall mean value of the response. This indicates how much the observed response’s deviation from the mean is accounted for by knowing the value of the predictor.

Lastly, the Sum of Squares Residual (SSR) $=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$, is the unexplained variability, an overall measure of how much the observed values of the response differ from the predicted values.

We use the sum of squares to calculate the coefficient of determination $R^2$

$$\begin{array}{}\text{(4.15)}& R^2=\frac{SSM}{SST}=1-\frac{SSR}{SST}\end{array}$$

Equation 4.15, shows that $R^2$ is a the proportion of variability in the response (SST) that is explained by the model (SSM). Note that $R^2$ is calculated as proportion between 0 and 1, but is reported as a percentage between 0% and 100%.

The $R^2$ in for the movie scores model in Equation 4.7 is 0.611. It is interpreted as the following:

About 61.1 % of the variability in the audience score for movies on Rotten Tomatoes can be explained by the model (critics score).

Your turn!

Do higher or lower values of $R^2$ indicate a better model fit?¹⁰

Similar to RMSE, there is no universal threshold for what makes a “good” $R^2$ value. When using $R^2$ to determine if the model is a good fit, take into account what might be a reasonable fit given the subject matter.

Your turn!

The $R^2$ for the movies model is 0.611. What is your evaluation of the model fit based on $R^2$? Explain your response.

4.7.3 Computing $R^2$ and RMSE in R

The glance() function in the broom package produces model summary statistics, including $R^2$. Recall from Section 4.4.2 that the movie scores model produced by the lm() function is saved as movie_fit.

glance(movie_fit)

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.611         0.608  12.5      226. 2.70e-31     1  -575. 1157. 1166.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

The code below will only return $R^2$ from the output of glance().

glance(movie_fit)$r.squared

[1] 0.6106479

RMSE can be computed using the rmse() function from the yardstick package (Kuhn, Vaughan, and Hvitfeldt 2025b). First, we use augment() from the broom package to compute the predicted value for each observation in the data set. These values are stored if the column .fitted. You may notice that many other columns are produced by augment() as well. We will discuss the statistics produced by augment() in depth in Chapter 6.

1movies_augment <- augment(movie_fit)

2rmse(movies_augment, truth = audience, estimate = .fitted)

1

Compute the predicted values (along with other observation-level model statistics) for the observations in the data and save the data frame as movies_augment.

2

Use movies_augment to compute RMSE, specifying column with the actual observed values (audience) and the column with the predicted values .fitted.

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard        12.5

Hickey, Walt. 2015. “Be Suspicious of Online Movie Ratings, Especially Fandango’s.” FiveThirtyEight, Available at: Http://Fivethirtyeight. Com/Features/Fandango-Movies-Ratings.

Kim, Albert Y., Chester Ismay, and Jennifer Chunn. 2018a. “The Fivethirtyeight r Package: ’Tame Data’ Principles for Introductory Statistics and Data Science Courses” 11. https://escholarship.org/uc/item/0rx1231m.

Kim, Albert Y, Chester Ismay, and Jennifer Chunn. 2018b. “The Fivethirtyeight r Package:‘tame Data’principles for Introductory Statistics and Data Science Courses.” Technology Innovations in Statistics Education 11 (1).

Kuhn, Max, Davis Vaughan, and Emil Hvitfeldt. 2025b. “Yardstick: Tidy Characterizations of Model Performance.” https://doi.org/10.32614/CRAN.package.yardstick.

———. 2025a. “Yardstick: Tidy Characterizations of Model Performance.” https://doi.org/10.32614/CRAN.package.yardstick.

Müller, Kirill, and Hadley Wickham. 2023. “Tibble: Simple Data Frames.” https://CRAN.R-project.org/package=tibble.

Pedersen, Thomas Lin. 2022. “Patchwork: The Composer of Plots.” https://CRAN.R-project.org/package=patchwork.

R Core Team. 2024. “R: A Language and Environment for Statistical Computing.” https://www.R-project.org/.

Robinson, David, Alex Hayes, and Simon Couch. 2023. “Broom: Convert Statistical Objects into Tidy Tibbles.” https://CRAN.R-project.org/package=broom.

Waring, Elin, Michael Quinn, Amelia McNamara, Eduardo Arino de la Rubia, Hao Zhu, and Shannon Ellis. 2022. “Skimr: Compact and Flexible Summaries of Data.” https://CRAN.R-project.org/package=skimr.

Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the Tidyverse” 4: 1686. https://doi.org/10.21105/joss.01686.

Wickham, Hadley, Mine Çetinkaya-Rundel, and Garrett Grolemund. 2023. R for Data Science. " O’Reilly Media, Inc.".

---

1. The response variable is audience , the audience score. The predictor variable is critics , the critics score.

2. Example: What do we expect the audience score to be for movies with a critics score of 75?

3. Example: Is the critics score a useful predictor of the audience score?

4. The population is all movies on the Rotten Tomatoes website. The sample is the set of 146 movies in the data set.

5. The interpretation of the intercept is meaningful, because it is plausible for a movie to have a critics score of 0 and there are observations with scores around 5, which is near 0 on the 0 - 100 point scale.

6. Source: https://www.rottentomatoes.com/m/barbie Accessed on August 29, 2023.

7. Source: https://www.rottentomatoes.com/m/asteroid_city Accessed on August 29, 2023.

8. The predicted audience score is 32.3155 + 0.5187 * 75 = 71.218. The model over predicted. The residual is 62 - 71.218 = -9.218.

9. Lower values indicate a better fit, with 0 indicating the predictor variable perfectly predicts the response.

10. Higher values of $R^2$ indicate a better model fit, as it means more of the variability in the response is being explained by the model.